Vyplatí se převést peníze jinam? Aneb vzoreček pro bankovní turisty

Jak rychle se začnou peníze úročit?
Převod peněz je stále rychlejší a výjimkou již nejsou ani okamžité platby, které jsou otázkou několika sekund. Běžnější je však lhůta „do druhého dne“, kdy převodem peněz z jednoho účtu na druhý ztratíme jeden den úročení. Mohou však nastat případy, kdy je výpadek delší. Typicky je to v situaci, kdy je nutno peníze nejprve převést na běžný účet s nízkým nebo nulovým úročením a z něj teprve na spořicí účet, případně je nutno jiným způsobem zasáhnout (nastavit výpovědní lhůtu a podobně). Ještě složitější situace bývá u jiných, méně používaných finančních nástrojů. Například Dluhopisy republiky je nutno zaplatit několik dní před jejich emisí (a tedy před začátkem jejich úročení).Je tedy na místě otázka, ve kterých případech se vyplatí převádět peníze z jednoho účtu na druhý. Je zřejmé, že
- Převodem peněz na jiný účet přijdeme o úrok za dobu potřebnou k převodu, případně i k dalším nutným úkonům.
- Ale na druhé straně účet s vyšším zhodnocením bude vynášet více, a po určité době tuto ztrátu dožene.
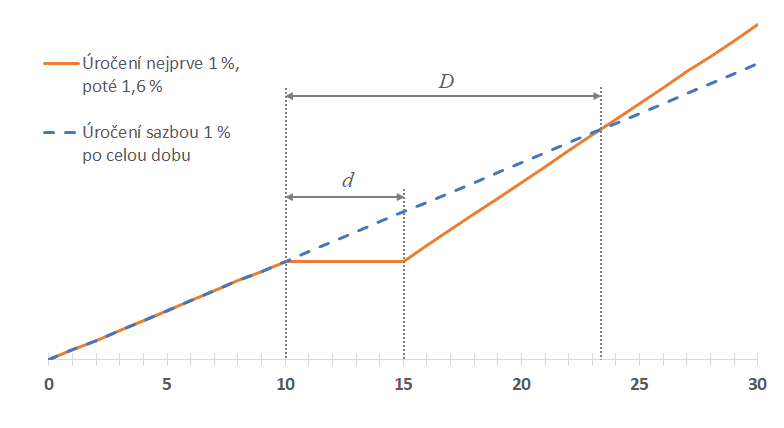
Na obrázku je příklad, kdy po dobu 10 dnů jsou peníze úročeny sazbou p1 = 1 %. Poté máme možnost převést je na jiný, výhodnější účet, kde budou úročeny sazbou p2 = 1,6 %, ale převod bude znamenat výpadek úroků po dobu d=5 dnů. Pokud převod provedeme, začnou úroky přibývat rychleji (oranžová čára) a po uplynutí D=13,3 dnů úroky doženou výpadek způsobený převodem a od této chvíle je úročení na novém účtu výhodnější. Znamená to tedy, že pokud víme, že peníze budou na novém účtu ještě nejméně 14. den od zahájení převodu, pak se nám převod vyplatí.
Jednoduchý vzoreček
Úloha se dá poměrně jednoduše a obecně spočítat. Při výpočtu použijeme zjednodušující předpoklad jednoduchého úročení, který znamená jen nepodstatnou nepřesnost. Přidržíme se již zavedeného označení, kde
p1 je úroková sazba „starého“ účtu,
p2 je úroková sazba „nového“ (výhodnějšího) účtu,
d je doba, po které nejsou peníze úročeny (například z důvodu převodu peněz),
D je počet dnů od zahájení převodu peněz, kdy vyšší úroky na novém účtu vyrovnají výpadek úroků.
Hledanou dobu D, po které se výnosy vyrovnají vypočítáme dle vzorce:
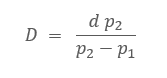
Je vidět, že ve vzorci vůbec nefiguruje objem peněz. To je v pořádku, protože výpočet nezávisí na tom, zda máme uloženou jednu korunu nebo milion. Doba D, po které se úroky srovnají, je přímo úměrná době d, kdy jsou naše peníze bez úroku. Naopak ve jmenovateli vzorku máme rozdíl úrokových sazeb p2 – p1. Čím menší bude tento rozdíl, tím delší dobu D budeme potřebovat. Pokud by byly obě úrokové sazby shodné (tj. p1 = p2) dostali bychom ve jmenovateli nulu. To je v pořádku, protože v takovém případě nový účet nikdy nedohoní ani sebemenší ztrátu způsobenou výpadkem úroků.
Výsledek výpočtu pro výchozí hodnotu p1 = 1 % a různé hodnoty p2 a d jsou v následující tabulce:
| Nová sazba p2 | d = 1 den | d = 2 dny | d = 7 dní | d = 14 dní |
| 1,10 % | 11,0 | 22,0 | 77,0 | 154,0 |
| 1,20 % | 6,0 | 12,0 | 42,0 | 84,0 |
| 1,30 % | 4,3 | 8,7 | 30,3 | 60,7 |
| 1,40 % | 3,5 | 7,0 | 24,5 | 49,0 |
| 1,50 % | 3,0 | 6,0 | 21,0 | 42,0 |
| 1,60 % | 2,7 | 5,3 | 18,7 | 37,3 |
| 1,70 % | 2,4 | 4,9 | 17,0 | 34,0 |
| 1,80 % | 2,3 | 4,5 | 15,8 | 31,5 |
| 1,90 % | 2,1 | 4,2 | 14,8 | 29,6 |
| 2,00 % | 2,0 | 4,0 | 14,0 | 28,0 |
Proč přesnost na desetiny dne?
V tabulce jsou dny uvedeny s přesností na jedno desetinné místo. Má to smysl, když obvykle není možné získat úroky za část dne? Důvod této zdánlivě zbytečné přesnosti je jiný.Ze vzorečku je patrné, že výsledná hodnota D je přímo úměrná délce výpadku úroků d. Toho můžeme využít při výpočtu potřebné doby D pro doby výpadku d, které v tabulce nejsou. Například při přechodu z účtu úročeného 1 % na účet se sazbou 1,4 % vychází pro jeden den D(1) = 3,5. Pro dva dny to tedy bude dvojnásobek: D(2) = 7 a pro 10 dnů desetinásobek D(10) = 35. Pro podobné účely je proto vhodné znát hodnotu D přesněji než na celé dny, protože násobením bychom zvětšovali nepřesnost vzniklou zaokrouhlením.
Jak je to s daněmi?
Další poznámka se týká daní. Vzoreček počítá s tím, že peníze jsou skutečně zhodnocovány sazbami, které jsou ve vzorečku použity. Většina podobných příjmů podléhá dani ve výši 15 %, takže pokud je například spořicí účet úročen nominální sazbou 1 %, náš skutečný výnos je pouze 0,85 %, což je také hodnota, kterou bychom měli ve vzorečku použít. Naštěstí si toto přepočítávání na čisté úroky po zdanění můžeme většinou ušetřit.Pokud je totiž zdanění u starého a nového účtu stejné (což je velmi pravděpodobné), pak není potřeba zdanění započítávat. Proč? Skutečné zhodnocení po zdanění spočítáme tak, že nominální sazbu vynásobíme hodnotou (1-daňová sazba), což například při 15% dani dá 0,85. Číslem 0,85 bychom měli vynásobit hodnoty sazeb p1 i p2. Když se však na vzoreček podíváme blíže, vidíme, že vynásobení obou sazeb stejným číslem výsledek neovlivní, protože se tyto členy jednoduše vykrátí. Pokud je tedy zdanění obou hodnot p1 i p2 stejné, můžeme do vzorce dosadit nominální úrokové sazby. Pouze v případě, že se zdanění liší, je nutno dosadit skutečné zhodnocení po zdanění.
Jak to vychází?
Když se podíváme do tabulky vidíme, že při běžném mezibankovním převodu který trvá jeden den se nemusíme příliš dlouho rozpakovat. I minimální rozdíl sazeb o desetinu procentního bodu nám dohoní jednodenní ztrátu za 11 dní, což je zpravidla dobře akceptovatelné.Pozor je však třeba dát při delších prodlevách. 14 dní je zřejmě extrém, ale pokud nám peníze nevydělávají jeden týden, pak i rozdíl 0,3 procentního bodu potřebuje k dohnání výpadku celý měsíc. A to už je dost.
Při posuzování je totiž nutno zvážit nejen dobu, po kterou chceme nechat peníze vydělávat, musíme také zvážit stabilitu nové úrokové sazby. Mohlo by se totiž stát, že peníze převedeme na jiný účet s tím, že je chceme nechat úročit ještě dva roky. Pokud je však na novém účtu proměnná úroková sazba, může se hned druhý den změnit a pak na transakci proděláme.
Autor: Petr Kielar










