Anuitní splátka

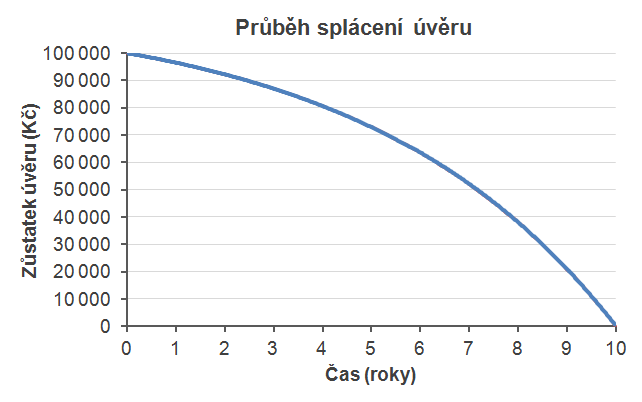
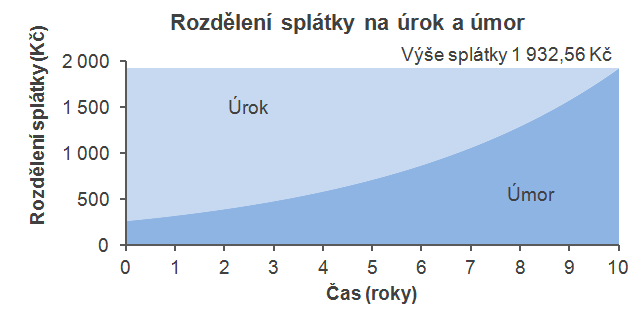
Dříve se jako anuita (annuita, ročina) označovala roční splátka úvěru. Dnes se tak označuje pravidelná splátka úvěru, která je obvykle měsíční a zahrnuje úrok za dané období i úmor (splátku jistiny).

Mohlo by vás zajímat

Anuitním způsobem splácení se rozumí způsob, při kterém se výše platby (anuity) nemění, mění se pouze poměr mezi úrokem a úmorem (na počátku je úrok největší a s postupem času klesá, naopak úmor je na počátku nejmenší a s časem roste). Naopak dlužná částka klesá zpočátku pomalu a s postupujícím časem se klesání zrychluje.

Typický průběh anuitního splácení úvěru. Zpočátku je pokles dlužné částky pomalý, protože velká část splátky se spotřebuje na splacení úroků. S postupem času dlužná částka klesá a s tím klesají i úroky. Díky tomu se postupně zvyšuje část splátky použitá na splacení (umoření) dlužné částky (úmor).

Při anuitním splácení se výše splátky nemění, zůstává konstantní po celou dobu splácení úvěru. Část splátky je použita ke splacení úroků, zbývající část snižuje dlužnou částku.

Výše anuitní splátky

Výši anuitní splátky je možno vypočítat podle následujícího vzorce: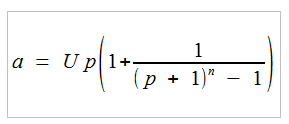

kde

a   je výše splátky
U   je výše úvěru (kladné číslo)
p   je úroková sazba za období
n   je počet období

Tento vzorec platí pro pravidelné polhůtní splácení, tedy pro splácení, kdy platba je provedena na konci období. Někdy se používá také vzorec pro předlhůtní splácení, kdy jsou splátky prováděny na počátku období (první splátka je tedy uhrazena současně s výplatou úvěru). Další podrobnosti včetně odvození najdete na stránce se vzorci pro úrokový počet. Pro výpočet anuitní splátky můžete také použít úvěrový kalkulátor.

Použití vzorce pro výpočet anuitní splátky

Při použití tohoto vzorce je potřeba dávat pozor na správné dosazení úrokové sazby p a počtu období n. Pokud je úvěr splácen ročními splátkami, za hodnotu p dosadíme roční úrokovou sazbu a n bude počet let.

Velmi často je však úroková sazba p roční, ale úvěr je splácen měsíčně, zajímá nás tedy výše měsíční splátky. Pak musíme do p dosadit měsíční úrokovou sazbu, která 1/12 roční úrokové sazby. Hodnota n bude počet měsíců.

Příklad

Úvěr ve výši 100 000 Kč je úročen roční úrokovou sazbou 6 % p. a. a má být splacen měsíčními splátkami za 10 let. Jaká je výše splátky?

Dosadíme

U = 100 000
p = 6 % / 12 = 0,5 % = 0,005
n = 10 × 12 = 120

a po dosazení dostaneme výsledek a = 1 110,21 Kč.

Vzorec je zjednodušený, realita bývá složitější

Výše uvedený vzorec pro výpočet anuitní splátky je zjednodušený. Předpokládá totiž, že všechna období jsou stejně dlouhá. To ale v praxi obvykle neplatí. Například při měsíčním splácení úvěru (které je u nás nejobvyklejší) narazíme hned na dva problémy: měsíce jsou různě dlouhé (mají 28 až 31 dnů) a také se může stát, že datum splátky připadne na den, kdy neprobíhá platební styk (víkendy, svátky) a platba pak musí proběhnout v jiný den.

A aby toho nebylo málo, existuje několik způsobů počítání kalendářních dnů. Banka používá jeden z těchto standardů a zpravidla se musíme velmi pozorně začíst do dokumentů abychom zjistili který to je.

Díky tomu se nám může stát, že když porovnáme výši splátky úvěru v úvěrové smlouvě s výpočtem podle zjednodušeného vzorce splátek, dojdeme k odlišným číslům. Rozdíly však nejsou velké a s ohledem na celkovou cenu úvěru bývají zanedbatelné.