Je pro vás RPSN užitečná informace, nebo jen číslo?

Roční procentní sazba nákladů, neboli RPSN je informace, která má sloužit zájemcům o úvěr jako měřítko ceny úvěru. Praxe je však taková, že pro řadu klientů je to nesrozumitelné číslo s nejasným významem a proto jej raději ignorují. Podívejme se blíže na to, jak je RPSN zavedena a jakou informaci nám poskytuje. V textu se neobejdeme bez matematických formulí, ale žádný strach. Vše je psáno tak, aby bylo možno složité výrazy ignorovat a číst pouze text.

Co je RPSN, aneb definice

Základním problémem RPSN je její komplikovaná definice. Ať chceme nebo ne, bez trochy matematiky se neobejdeme. RPSN je totiž definována jako řešení následující rovnice: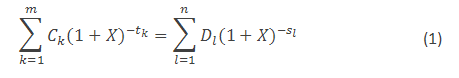 kde X je hledaná hodnota RPSN, C_k jsou jednotlivá čerpání (výplaty) úvěru a D_l platby klienta. t_k je časový interval mezi prvním a k-tým čerpáním úvěru a s_l je časový interval mezi prvním čerpáním a okamžikem, ve kterém je provedena l-tá platba klienta. Přitom čas se měří v rocích.

Tato definice je pro většinu lidí odstrašující a to je pravděpodobně jedním z důvodů, proč je RPSN zahalena takovým tajemstvím. Existuje řada náhradních definic, které se snaží RPSN popsat slovně a tak přiblížit tuto problematiku lidem, kteří si nelibují v matematice. Tyto popisné definice jsou však zpravidla buď nesprávné, nebo nesrozumitelné, někdy obojí. Snad nejsprávnější slovní popis této rovnice zní takto: RPSN je úroková sazba, při které je současná hodnota všech peněžních toků spojených s úvěrem rovna nule. I tato definice je však srozumitelná pouze úzkému okruhu lidí, obeznámených s finanční matematikou. Spokojme se proto s konstatováním, že RPSN je definována jako řešení rovnice (1) a podívejme se, jaké má RPSN díky tomu vlastnosti.

Jednoduchý příklad

Předpokládejme úvěr ve výši 100 korun. Pro jednoduchost nebude úvěr postupně umořován, ale bude splacen po roce jedinou splátkou ve výši 110 korun. To odpovídá situaci, kdy je vypůjčená částka úročena deseti procenty a v průběhu roku se nepočítají úroky z úroků. Jaká je hodnota RPSN?

Když dosadíme do základní rovnice, dostaneme Protože je úvěr vyplacen v plné výši jedinou platbou, bude na levé straně jediný člen. Čas první výplaty úvěru je dle definice nula, takže t₁=0 a libovolné číslo umocněné na nultou je 1.

Na pravé straně bude rovněž jediný člen odpovídající platbě klienta. Tato platba je provedena po uplynutí jednoho roku od čerpání, tedy s₁=1. Zbývá si uvědomit, že
( 1 + X )^-1 = 1 / ( 1 + X ) poměrně jednoduchý výraz

ze kterého snadno spočítáme, že X = 0,1, neboli RPSN = 10 %. V tomto případě Hodnota RPSN je rovna nominální úrokové sazbě skutečně pouze ve speciálních případech. Jak si ukážeme dále, obecně to neplatí. je tedy RPSN rovna nominální úrokové sazbě. K čemu je tedy RPSN dobrá?

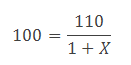
RPSN zohledňuje poplatky

Představme si, že banka přijme kreativního marketingového odborníka, který zjistí, že klienti nechtějí platit vysoké úroky. Banka proto začne nabízet úvěry ve výši 100 korun s nulovým úrokem, ale přidá poplatek. Klient po roce splatí úvěr splátkou ve výši 100 korun (úrok je nulový), ale k tomu přidá poplatek 10 korun. Výsledek je pro klienta stejný (po roce zaplatí opět 110 korun), ale úvěr je skutečně úročen nulovou sazbou. Jaká bude v tomto případě hodnota RPSN? Platby klienta budou stejné, pouze budou rozděleny na dvě části (splátka a poplatky). Když dosadíme do rovnice (1), dostaneme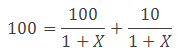 Matematicky tedy dojdeme opět k výsledku RPSN = 10 % což je dobře. Údaj o RPSN byl totiž zaveden právě z těchto důvodů, aby zahrnul do jediného čísla všechny náklady (platby) klienta, které s úvěrem souvisí. Nezáleží na tom, jak bude platba klienta nazvána (zda úrok, poplatek, nebo například „záporný bonus“), vždy bude do výpočtu zahrnuta stejným způsobem.

RPSN však není totéž, co úroková sazba

Zdálo by se tedy, že RPSN je vlastně úroková sazba, do které jsou zahrnuty všechny poplatky, případně další související náklady úvěru. Tak jednoduché to však není. RPSN sice zahrnuje všechny náklady související s úvěrem, ale navíc ještě převádí úrokovou sazbu na stejný způsob úročení. Co to znamená?

Všimněme si, že úvěr, který jsme použili v předchozích příkladech, byl úročen tak, že se úroky připisovaly k jistině jednou za rok, a to přesně rok od čerpání úvěru. V praxi se však úroky připisují k jistině na konci kalendářního roku. Co by se tedy stalo, kdyby byl náš ukázkový účet vyplacen v polovině roku?

Na konci kalendářního roku (tedy po šesti měsících) by banka spočítala úroky a připsala je k jistině. A druhý půlrok by se úročila částka zvýšená o tento úrok. Úrok za první půlrok bude v našem případě 5 korun (polovina ročního úroku). Ve druhém půlroku tedy budeme počítat úrok z částky 105 korun, což je (opět za polovinu roku) 5,25 koruny.

Úvěr ve výši 100 korun je tedy po roce splacen splátkou 110,25 koruny – klient zaplatí o 25 haléřů více, pokud si nechá úvěr vyplatit v polovině roku. To se projeví i v hodnotě RPSN. Dosazením do rovnice (1) totiž dostaneme

takže X = 0,1025 a tedy RPSN = 10,25 %. Úroková sazba úvěru se nezměnila, ale klient zaplatí za úvěr více a to se odrazí i v hodnotě RPSN.

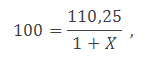
Tento příklad můžeme interpretovat tak, že pokud klient získá úvěr, který se úročí jednou ročně, je pro něj výhodnější, když tento úvěr čerpá na začátku kalendářního roku, než v jeho polovině. Pokud je úvěr vyplacen na začátku roku, klient zaplatí méně a tomu odpovídá i nižší hodnota RPSN.

Měsíční připisování úroků vyjde také odlišně

Zřejmě není potřeba podrobně počítat co se stane, pokud jsou úroky z úvěru připisovány k jistině jindy, než jednou ročně. V ČR se obvykle připisují úroky na konci měsíce, takže za vyplacených 100 korun je po roce úročení nutno splatit celkem 110,47 koruny (každý měsíc počítáme úrok a úroky z úroků). Pak bude hodnota RPSN rovna 10,47 % což odpovídá skutečnosti, že klient zaplatí o něco více, než v případě, kdy jsou úroky počítány a připisovány k jistině jen jednou ročně.

RPSN počítá úroky jinak, než banka

Platí tedy, že RPSN je rovna nominální úrokové sazbě alespoň tehdy, když jsou úroky připisovány ve stejných intervalech, jak definuje RPSN (tedy jednou ročně)? Bohužel, ani toto neplatí. Podívejme se co se stane, pokud úvěr trvá kratší dobu, než je jeden rok. Budeme opět předpokládat, že úvěr je úročen sazbou 10 % a úroky jsou připisovány k jistině jednou ročně. Nyní již víme, že je důležité i to, ve kterém měsíci je úvěr poskytnut. Proto předpokládejme, že výplata úvěru proběhne v lednu a úvěr bude splacen po šesti měsících, takže až do splacení úvěru není jistina zvyšována o úroky.

Po šesti měsících jsou úroky z úvěru přesně 5 korun (polovina z 10 %), takže klient splatí 105 korun. Jaká bude hodnota RPSN? Opět dosadíme do rovnice (1) a  dostaneme Číslo umocněné na -0,5 je totéž, jako druhá odmocnina obrácené hodnoty. Tedy
( 1 + X)^-½ = 1 / √( 1 + X )

takže X = 0,1025 a tedy RPSN = 10,25 %. Co se stalo? I když v průběhu splácení nedošlo k připsání úroků, hodnota RPSN je jiná, než nominální úroková sazba.

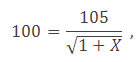
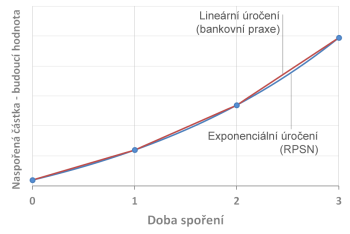
Čím je to způsobeno? Zjednodušeně řečeno, vzorec pro výpočet RPSN počítá s tím, že úroky na úvěrovém účtu narůstají exponenciálně. Takový způsob úročení však není běžný. Obvyklý způsob úročení je takový, že do doby, než jsou připsány úroky, narůstá úrok lineárně. Pak dojde k připsání úroků což způsobí, že v dalším období rostou úroky sice opět lineárně, ale rychleji. Když porovnáme exponenciální úročení, které používá rovnice pro výpočet RPSN s úročením, které používají banky, zjistíme, že v okamžicích, kdy se připisují úroky, dostaneme stejné hodnoty, ale v období mezi těmito okamžiky se obě hodnoty liší.

Co tedy RPSN vlastně ukazuje?

Na RPSN se tedy můžeme dívat jako na číslo, které nějakým způsobem hodnotí cenu úvěru a přitom bere do úvahy i časovou hodnotu peněz. To je poněkud vágní a neurčité konstatování, nicméně i toto má svou hodnotu. Pokud jsou klientovi nabídnuty dva úvěry se stejnou výší a stejnou (nebo alespoň podobnou) dobou splatnosti, je možno RPSN použít jako měřítko jejich výhodnosti.

RPSN jednoho úvěru však nelze srovnávat s úrokovou sazbou jiného úvěru, a to ani v případě, kdy se jedná o úvěr poskytovaný bez poplatků. V předchozích odstavcích jsme viděli, jak se může hodnota RPSN měnit v závislosti na způsobu úročení. Na RPSN může mít vliv i okamžik, kdy je úvěr poskytnut.

Bylo by příjemné, kdybychom mohli říci, že RPSN je úroková sazba, která pouze zahrnuje do úrokové sazby veškeré náklady, které s úvěrem souvisí. To je ale pouze část pravdy. RPSN totiž navíc převede úrokovou sazbu na jiný, standardizovaný způsob úročení. Jen tak je možno zajistit srovnatelnost RPSN u různých finančních produktů, které používají různé způsoby úročení. Jedinou (avšak citelnou) nevýhodou takového postupu je skutečnost, že tento standardizovaný způsob úročení není v praxi používán. Proto je hodnota RPSN tak obtížně uchopitelná a proto je nutno vzájemně srovnávat pouze hodnoty RPSN. To je také důvod, proč stavebky.cz používají koncept čisté úrokové sazby, která vychází z měsíčního připisování úroků, což je v ČR obvyklá praxe. Proto je čistá úroková sazba pro porovnávání úvěrových (ale i spořicích) produktů výhodnější.

A jak RPSN spočítat?

V tomto článku jsme použili extrémně jednoduché příklady a díky tomu jsme byli schopni rovnici (1) vyřešit. Pokud by měl úvěr dvě splátky, dostali bychom kvadratickou rovnici, jejíž řešení je sice obtížnější, ale dá se zvládnout pomocí vzorečku ze střední školy. V praxi však v rovnici (1) figurují desítky až stovky splátek. Takový výpočet je možný pouze numerickými metodami pomocí počítače. Na stavebkách.cz najdete několik kalkulátorů, které takové výpočty umí provést.

• Úvěrová kalkulačka vychází ze známé úrokové sazby a délky splatnosti úvěru. Po zadání výše úvěru a poplatků vypočítá kromě RPSN také výši měsíční splátky a čistou úrokovou sazbu.
• Pokud známe kromě výše úvěru a doby splatnosti také výši měsíčních splátek a poplatků, nepotřebujeme již znát úrokovou sazbu úvěru. Kalkulátor čisté úrokové sazby vypočítá i RPSN.
• Pro zcela obecné řešení rovnice (1) slouží kalkulátor RPSN peněžních toků. Vypočítá hodnotu RPSN z měsíčních (nebo ročních) obratů – čerpání úvěru a splátek.

Autor: Petr Kielar