Peníze i viry se množí exponenciálně. Proč je tedy milionářů méně, než nemocných?

Jak roste počet nakažených?
Nejprve se podívejme na jednoduchý model šíření nemoci. Řekněme, že každý nemocný nakazí dva jiné, dříve zdravé jedince. Na začátku máme jednoho nemocného, který v prvním kroku nakazí dva další. Ve druhém kroku každý z těch dvou nakažených přenese nemoc na další dva, takže máme čtyři nově nakažené. A tak to pokračuje dál a dál.
Toto šíření se dá snadno popsat exponenciální funkcí.
| 0. krok | 1 | 1. krok | 1 × 2 = 1 × 21 = 2 | 2. krok | 1 × 2 × 2 = 1 × 22 = 4 | 3. krok | 1 × 2 × 2 × 2 = 1 × 23 = 8 | … | n-tý krok | 1 × 2 × 2 × 2 … = 1 × 2n |
Což se dá zobecnit tak, že počet nově nakažených v n-tém kroku bude
kde N0 je počet nakažených na začátku (tedy v nultém kroku) a R je reprodukční číslo. A právě reprodukční číslo určuje chování exponenciály. Pokud je vyšší než 1, pak exponenciála roste, naopak pro R menší než 1 exponenciála klesá. A pro R = 1 je konstantní.
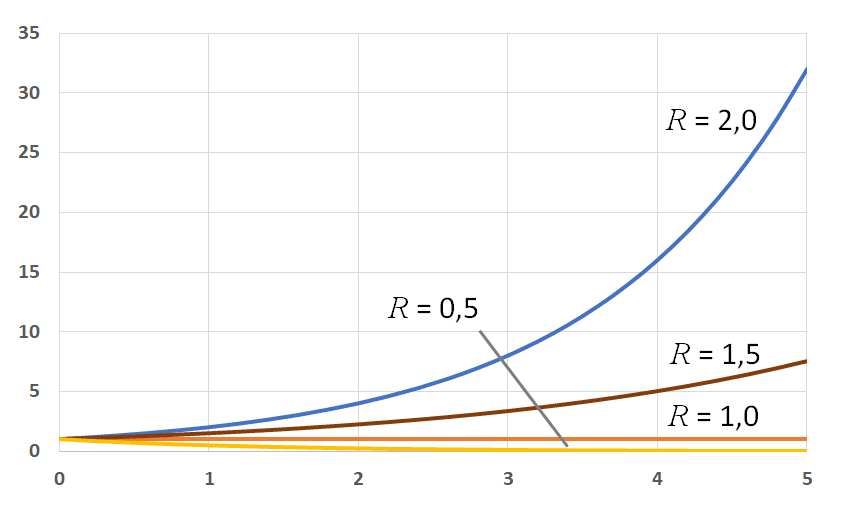
Exponenciála roste rychle
Bouřlivé debaty kolem aktuální koronavirové pandemie jsou v zásadě způsobeny tím, že pokud je reprodukční číslo R větší než jednička, exponenciální funkce, která popisuje počet nakažených, roste rychle. Velmi rychle. Popularitu dodává exponenciální funkci anekdota o vynálezci šachu. Ten pěkně napálil svého panovníka, který ho chtěl za vynález této kratochvíle odměnit. Autor hry požádal, aby jako odměnu obdržel šachovnici, na které by bylo jedno obilné zrnko na prvním políčku. Na druhém dvojnásobek, tedy dvě zrnka, na dalším opět dvojnásobek, a tak dále.Fakt je, že exponenciální růst je velmi rychlý a ze školy si možná pamatujeme, že exponenciála roste rychleji než polynom libovolného stupně. I když to tak třeba na první pohled nevypadá. Když exponenciální funkci 2n porovnáme například druhou mocninou n2, nevypadá to zpočátku přesvědčivě. Druhá mocnina je na počátku (pro n=0) nulová, zatímco exponenciála startuje na jedničce. Druhá mocnina ale tento handicap rychle dožene a pro n=2 jsou hodnoty vyrovnané a pořadí se obrací. Pro n=3 má exponenciála hodnotu 23 = 8, zatímco 32 = 9.
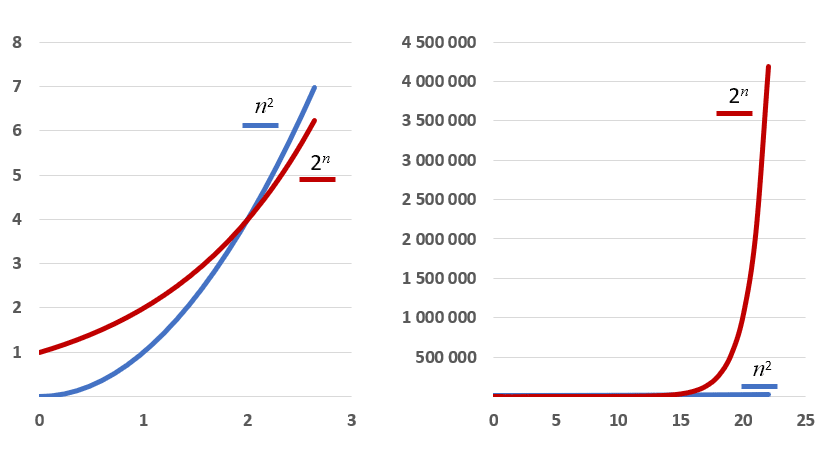
Stačí však chvilku počkat. V hodnotě n=4 se hodnoty opět vyrovnají a pro vyšší n je již exponenciála vždy vyšší.
| n | n2 | 2n |
| 0 | 0 | 1 |
| 1 | 1 | 2 |
| 2 | 4 | 4 |
| 3 | 9 | 8 |
| 4 | 16 | 16 |
| 5 | 25 | 32 |
| … | … | … |
| 10 | 100 | 1024 |
| 20 | 400 | 1048576 |
Někdo by mohl namítnout, že druhá mocnina je málo. Taková stá mocnina (tedy n100 roste rychleji. Ale dá se ukázat Důkaz není složitý, ale není jednoduché na něj přijít. Vezměme podíl P(n)/ exp(n) kde P je libovolný polynom a exp exponenciální funkce. A hledáme limitu podílu pro n→∞. Dostaneme neurčitý výraz, na který opakovaně použijeme l’Hospitalovu větu. Zatímco čitatel se nám po několika derivacích vynuluje, exponenciála ve jmenovateli zůstane beze změn. ■ , že i když vezmeme sebevětší mocninu, na exponenciálu je krátká. Vždy existuje hodnota n, pro kterou se exponenciála ujme vedení a už se nenechá předběhnout.
Exponenciála kam se podíváš
Exponenciální funkce popisuje nejen šíření infekčních chorob, ale i řadu dalších jevů. Obrázek podobný tomu prvnímu (o šíření infekce) najdeme i v učebnici fyziky, kde popisuje řetězovou jadernou reakci. Jen místo postaviček najdeme jádra uranu a namísto virů poletují neutrony. Exponenciální funkce popisuje množení virů, bakterií, králíků i lidí.Proč tedy není Země už dávno přeplněná všemi těmi viry, bakteriemi, králíky a lidmi? Příroda nemá ráda extrémy a při exponenciálním růstu se dříve nebo později začne z různých důvodů reprodukční číslo snižovat. V jaderném reaktoru vyhoří štěpný materiál, králíkům dojde seno. Ani počet nemocných nemůže být vyšší, než je počet lidí na planetě. Exponenciální funkce tedy obvykle popisuje růst velmi přesně, ale pouze za určitých předpokladů. Změna reprodukčního čísla může rychlý růst zpomalit i zrychlit, nebo naopak zvrátit v pokles. Ostatně proto také dnes držíme karanténu.
I úroky nabíhají exponenciálně
Je zajímavé si uvědomit, že exponenciálně se množí také peníze. Když uložíme jednu korunu na účet s desetiprocentním úrokem, budeme mít za rok 1 ×1,1 =1,1 Kč. Za dva roky se nám už budou počítat úroky z úroků, takže dostaneme 1 ×1,1 ×1,1 =1,21 Kč a tak dále. Po uplynutí n let tedy budeme mít na účtu
což nápadně připomíná vzoreček pro počet nově nakažených uvedený výše. Skutečně je to tak: vzoreček pro výpočet budoucí hodnoty má stejný tvar. Naspořenou částku N po uplynutí n roků spočítáme dosazením do vzorečku
kde N0 je počáteční zůstatek a reprodukční číslo R je úroková sazba zvýšená o jedničku (R = 1 + i). Vzoreček je stejný jako ten, který popisuje počet nově infikovaných pacientů! Neodbytně se však vnucuje otázka: když se peníze množí exponenciálně, stejně jako viry, jak je možné, že jsem každou chvíli nemocný, ale nejsem milionář?
Důvody, proč je jednodušší chytit rýmu, než vydělat na úrocích milion, jsou dva. Prvním důvodem je hodnota reprodukčního čísla. U chřipky nebo dnes populárního Covidu-19 se pohybuje kolem dvojky (pokud nečiníme ochranná opatření typu karantény a podobně), u spalniček se uvádí dokonce hodnota 18. Peníze mají reprodukční číslo velmi blízké jedničce. Za dobrý úrok je dnes považováno jedno procento, což znamená reprodukční číslo R = 1,01. A čím více se reprodukční číslo blíží k jedničce, tím více se exponenciála blíží ke konstantě.
Zatímco běžná respirační nemoc potřebuje k infikování další skupiny nešťastníků několik dnů, vklad na účtu se zvýší o roční úrok za 12 měsíců. Když jeden nemocný infikuje své okolí během jednoho týdne, pak za rok (pokud není nařízena karanténa) tady máme 52. generaci nových pacientů. A tento rozdíl je již znát.
Autor: Petr Kielar