Pravidlo 72, aneb jak spočítat zhodnocení investice bez kalkulačky

Znáte Pravidlo 72? Pokud chceme zjistit, za jak dlouho se naše investice zdvojnásobí, stačí vzít číslo 72 a vydělit ho ročním zhodnocením vaší investice v procentech. Výsledek nám řekne, kolik let budeme muset čekat, než se investice zdvojnásobí. Pokud se například náš vklad bude zhodnocovat 4 % každý rok, pak spočítáme 72 : 4 = 18 a zjistíme, že za 18 let budeme mít dvojnásobek. Je to zajímavé a funguje to docela přesně. Zajímá vás proč?

Pravidlo 72

Je to zajímavá pomůcka, jejímž autorem je pravděpodobně italský františkánský mnich Luca Pacioli (1447-1517). Řeší otázku, jak jednoduše spočítat dobu, za kterou se naše investice zdvojnásobí. Předpokladem je, že známe roční zhodnocení naší investice, které se nemění. Jde tedy o úlohu matematickou, nikoli o prognózu úrokových sazeb nebo akciových indexů.

Finanční matematika tuto úlohu řeší, ale je k tomu potřeba logaritmování – ostatně blíž se na to podíváme ve druhé (zajímavější) části tohoto článku. Pravidlo 72 je zajímavé tím, že tento úkol můžeme zvládnout výpočtem z hlavy a zkušený finanční poradce může tuto znalost využít pro vyvolání úžasu u svého klienta. A naopak: informovaný klient může s pomocí Pravidla 72 přivést méně erudovaného poradce do nepříjemných rozpaků.

Pravidlo říká, že počet let potřebných pro zdvojnásobení investice zjistíme tak, že číslo 72 vydělíme úrokovou mírou v procentech. Například:

Pravidlo lze přirozeně použít i obráceně: pokud je naším cílem zdvojnásobit investici za určitý počet let, stačí vydělit číslo 72 počtem roků a dostaneme potřebné roční zhodnocení v procentech. Například takto:

Když si Pravidlo 72 ověříme výpočtem, zjistíme, že funguje překvapivě přesně. Na následujícím grafu je modrou čarou vynesena závislost doby do zdvojnásobení investice vypočtená standardními vzorci finanční matematiky. Jednotlivé body jsou pak hodnoty vypočtené pomocí Pravidla 72.

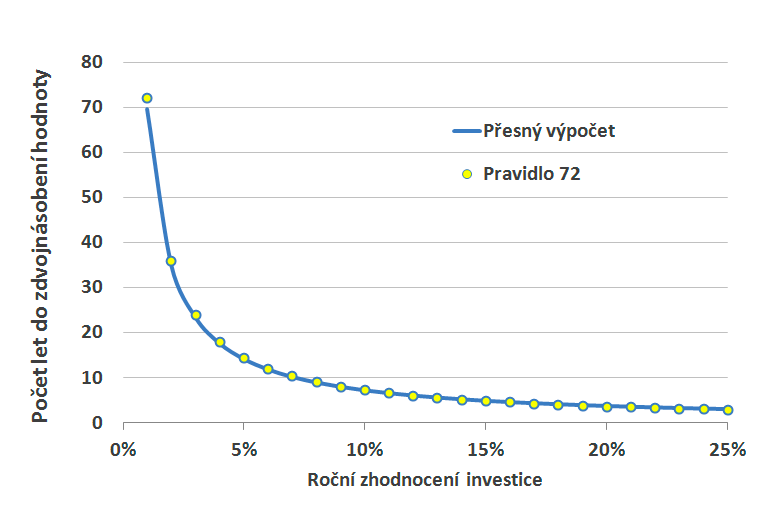
Vidíme, že body jsou skutečně velmi blízko přesnému výpočtu. Největší chybou je zatížen první bod, odpovídající úrokové míře 1 %. Pravidlo 72 zde dává výsledek 72, zatímco přesný výpočet ukazuje na hodnotu 69,66 roku. Pro dvouprocentní zhodnocení je chyba jen necelý rok a pro vyšší zhodnocení je chyba ještě menší.

Jak funguje Pravidlo 72?

Pravidlo 72 je pěknou ukázkou středoškolské matematiky, proto si neodpustím alespoň stručné vysvětlení. Běžný vzorec finanční matematikyOdvození je triviální, ponechávám na čtenáři. nám říká, že pokud investujeme částku j₀ s ročním zhodnocením p, pak po n letech bude hodnota investice

Protože si přejeme získat po n letech dvojnásobnou hodnotu původní investice, znamená to

z čehož můžeme vyjádřit hledaný počet let

Vyjde nám tedy poměrně jednoduchý vzoreček, jehož jediným problémem je výpočet logaritmu. V čitateli je přirozený logaritmus dvojky, což je přibližně 0,693, ale ve jmenovateli bychom museli logaritmovat úrokovou míru zvětšenou o jedničku. S kalkulačkou to není těžké, ale z hlavy umí logaritmovat jen málokdo. Jak to tedy zjednodušit?

Taylorův rozvoj

Každého asi napadne aproximovat logaritmus ve jmenovateli Taylorovým rozvojem. Pokud nemáte rádi matematiku, neděste se. Použijeme pouze první člen Taylorova rozvoje, tedy nahradíme logaritmus přímkou. V okolí bodu 1 je to totiž velmi jednoduché. Pro hodnoty x, které nejsou příliš vzdáleny od jedničky platí, že ln(x) ≈  x−1. Výsledek vidíme na obrázku níže. Modrou čarou je znázorněn logaritmus a červená přímka je aproximace prvním členem Taylorovy řady.

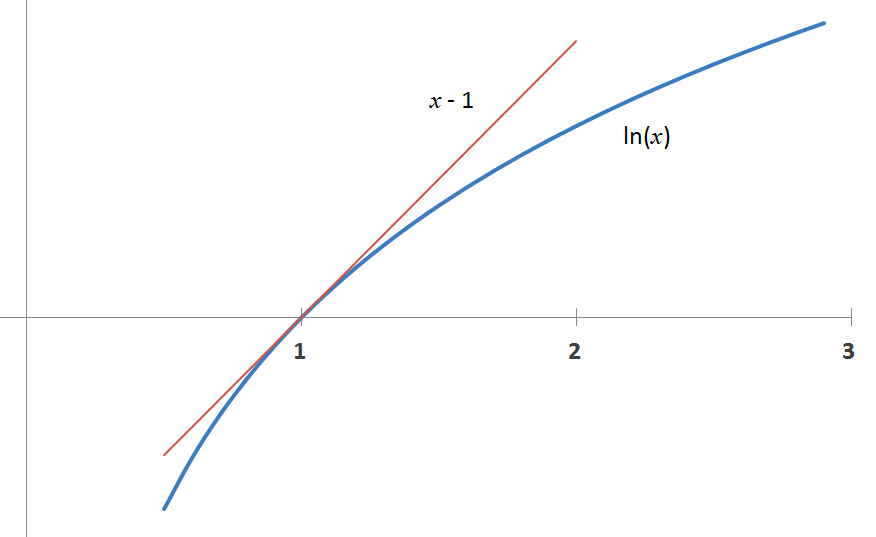
Je vidět, že v okolí jedničky je skutečně možné aproximovat logaritmus přímkou. A ve vzorečku (1) máme ve jmenovateli výraz ln(1+p), kde p je malé číslo, takže tato aproximace by mohla být docela dobrá. Když tuto aproximaci dosadíme do (1) a vyčíslíme hodnotu ln(2), dostaneme

To vynásobení stovkou je tam proto, abychom mohli při výpočtu z hlavy zadávat úrokovou míru v jednotkách procent. Výsledek je podobný pravidlu 72 až na to, že zde nemáme ono magické číslo 72, ale 69. Proč?

Optimalizujeme na (přibližně) 8 %

Logaritmus jsme aproximovali přímkou v okolí bodu 1. To ovšem znamená, že aproximace bude dávat nejpřesnější výsledky pro úrokové míry p v okolí hodnoty nula. A to se nám tak docela nehodí, protože zhodnocení investice p bude sice malé číslo, ale nebude nula a rozhodně nebude zápornéSamozřejmě že můžeme mít investici, jejíž zhodnocení je nulové, nebo dokonce záporné. Ale hodnota takové investice nikdy nevzroste na dvojnásobek – což je naše zadání. Proto pro nás nejsou podobné hodnoty zajímavé. . Proto by bylo vhodné aproximaci vylepšit tak, aby byla co nejpřesnější pro nějakou obvyklou hodnotu p. Volba padla na číslo p≈0,0785, tedy 7,85 %. V praxi to znamená, že přímku pomocí které aproximujeme logaritmus poněkud nakloníme, takže není tečnou k logaritmu v bodě 1, ale sečnou. Přímka protne funkci logaritmu v bodech x=1 a x=1,0785. Výsledek je na následujícím detailním obrázku. Vzhledem k tomu, že rozdíl mezi logaritmem a přímkou je skutečně velmi malý, jde o náčrtek, který je úmyslně zdeformovaný. Jinak by na obrázku byly pouze tři překrývající se čáry.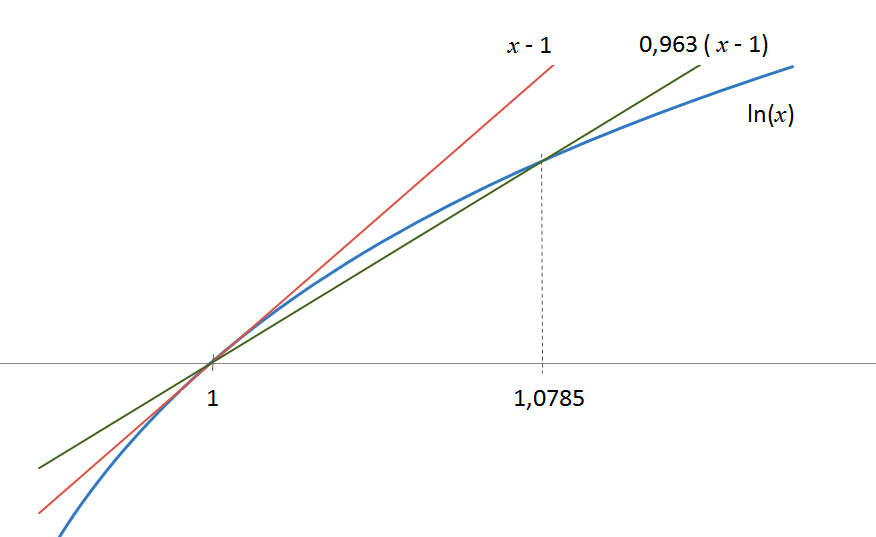

Tímto způsobem dostaneme jinou aproximaci, kterou když dosadíme do (1), dostaneme

což už je naše hledané Pravidlo 72. Oproti předchozímu vzorci (2) dává nejpřesnější výsledky pro úrokové míry blízké 8 % (přesněji 7,85 %). O tom se ostatně můžeme snadno přesvědčit. Stačí když si do grafu vyneseme rozdíl mezi přibližným a přesným výpočtem pro různé hodnoty úrokové míry p.

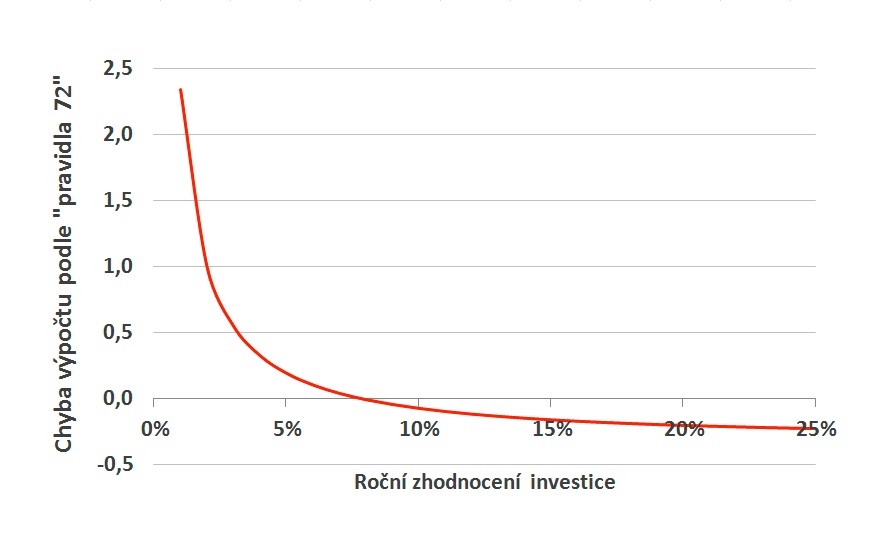
Jak už jsem zmínil v komentáři k prvnímu grafu, nejvyšší odchylka je u nejnižších hodnot úrokové míry. Při 1% zhodnocení se použitím Pravidla 72 dopustíme chyby 2,3 roku a pro nižší hodnoty tato odchylka dále prudce narůstá. Ale pro vyšší hodnoty p chyba rychle klesá a nulová je  právě pro p=0,0785. Tam graf protíná osu x a míří do záporných hodnot. Pro úrokové míry vyšší než 7,85 % se chyba opět zvětšuje Pro pořádek musím dodat, že pro zhodnocení vyšší než 96,7 % se chyba začne opět snižovat a pro nekonečně vysoké zhodnocení dá Pravidlo 72 opět přesný výsledek (nulu). , jen má záporné znaménko.

Optimální zhodnocení lze nastavit

Z předchozího grafu je patrné, že pro velmi nízké úrokové míry nedává Pravidlo 72 nejlepší výsledky. Ale tomu se dá odpomoci. Pokud bychom chtěli použít zjednodušený výpočet pro úrokové míry nižší než 8 %, můžeme hodnotu 72 snížit o jedničku na každé tři procentní body, o které se vzdálíme od 8 %. A naopak – pokud bude zhodnocení investice vyšší než 8 %, můžeme k číslu 72 přičíst jedničku na každé tři procentní body, které jsou nad 8 %. Tedy například pokud bude zhodnocení 5 %, použijeme namísto 72 číslo 71.

Takto lze výpočet zpřesnit, ale nemyslím si, že by to někdo dělal. Kalkulačky a počítače jsou dnes natolik dostupné, že podobné vylepšování nemá smysl. Ale pokud jste přetrpěli předchozí odstavce s trochou matematiky, asi je vám jasné, proč to tak funguje. A to potěší.

Proč právě 72?

Ze způsobu odvození je zřejmé, že na rozdíl od Ludolfova čísla π nebo Eulerova čísla e, číslo 72 vlastně není nijak důležité číslo s neotřesitelnou pozicí. Pro číslo 72 vychází výpočet nejpřesnější v okolí 8% zhodnocení, ale stejně tak můžeme používat číslo 73 pro zhodnocení investic v okolí 11 %. To by nepochybně potěšilo Sheldona Coopera z oblíbeného sitcomu Teorie velkého třesku, podle kterého je 73 bezkonkurenčně nejlepší číslo. Stejně tak bychom se mohli držet více při zemi a používat hodnotu 71, která je optimální pro úrokové míry kolem 5 %. Číslo 72 má však jednu velkou výhodu – je dělitelné mnoha čísly (72 = 2×2×2×3×3) a to je pro počítání z hlavy k nezaplacení. Předpokládám, že to je hlavní důvod, proč se traduje právě Pravidlo 72 a ne jiné. Používáme ho totiž v situaci, kdy nemáme po ruce kalkulačku a kdy rychlost výpočtu je důležitější, než jeho přesnost.

Autor: Petr Kielar